Mesh Parametrization
Mesh parametrization is an interesting technique in digital geometry processing which lays foundations of widely known texture mapping technique in computer graphics field. As we know texture mapping idea is very straightforward, it works like wrapping a 3D model with a paper in real life where paper is our desired pattern to be shown in 3D model. To realize such technique in digital, we need coordinates to sample our texture image in order to color associated parts of our model with the desired texture pattern. To obtain such texture coordinates, mesh parametrization comes into play, we unfold 3D mesh onto a 2D plane of interest and compute associated texture coordinates.
Figure-1: An example mesh parametrization [1]
To obtain a parametrization as illustrated in Figure-1, there exists methods in literature that represents mesh parametrization problem as linear system [2]. Main idea is as follows:
- Mesh should not be a closed mesh.
- In an open mesh there exists boundary vertices
- Boundary vertices should be placed to a known 2D region
boundary (e.g. disk, rectangle)
- Knowing boundary vertex positions, we model the unknown vertex positions
by their first ring neighborhood. In other words, we know that a vertex in 3D mesh
should reside close to its neighborhood in parametrized 2D region.
- By applying convention in step above we construct a linear system,
and solution of this system for both (x,y) coordinates gives us
locations of non-boundary vertices in parametrized 2D region
Figure-2: In parametrized mesh, position of Vi is found by cumulative weighted sum of vectors coming to Vi. In other words linear system is constructed by convention illustrated in this figure
We can formalize the linear system by convention given in Figure-2 and idea above as follows:
$
Wx = b_x\\
Wy = b_y\\
$
$W_{ij} = \begin{cases}
1 & (i,j) \in E, i\notin B \\
-\sum{w_{ij}} & (i,i), i \notin B \\
1 & (i,i), i \in B \\
0 & otherwise
\end{cases}\\
$
$({b_x})_{i} = \begin{cases}
{V_i(x)} & i \in B \\
0 & otherwise
\end{cases}\\
$
$({b_y})_{i} = \begin{cases}
{V_i(y)} & i \in B \\
0 & otherwise
\end{cases}\\
$
where $B$ is set of boundary vertices, $(i,j)$ denotes edge between vertex $V_i$ and $V_j$ and $E$ is the edge set of original mesh, $V_i(x)$ and $V_i(y)$ x and y coordinate values of vertex $V(i) \in B$. Finally $x$ and $y$ vectors in equations are parametrized vertex coordinates. An example of this system where $W_{ij}$ values are uniform and set to 1 is illustrated below in Figure-3.
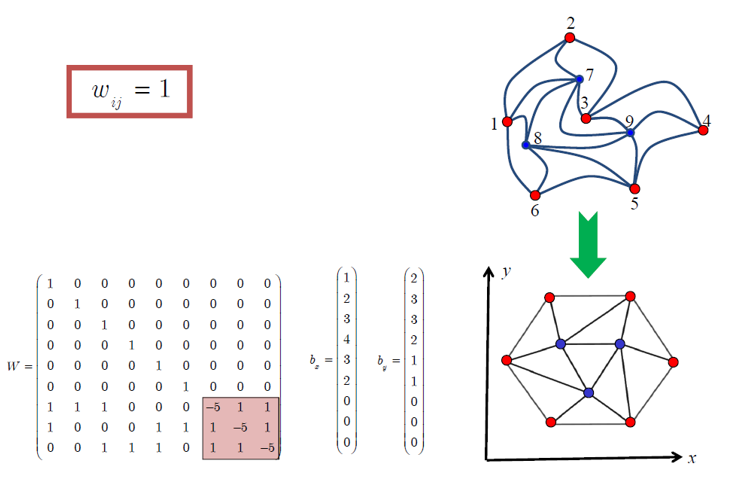
Figure-3: Example linear system for mesh parametrization using uniform $W_{ij} = 1$ values where red vertices are boundary vertices.
Hence solution to linear system both for $x$ and $y$ coordinate values become as follows:
$
x = W’b_x\\
y = W’b_y\\
$
Where $W’$ is inverse of $W$ matrix.
Figure-3: Different weight functions used in mesh parametrization
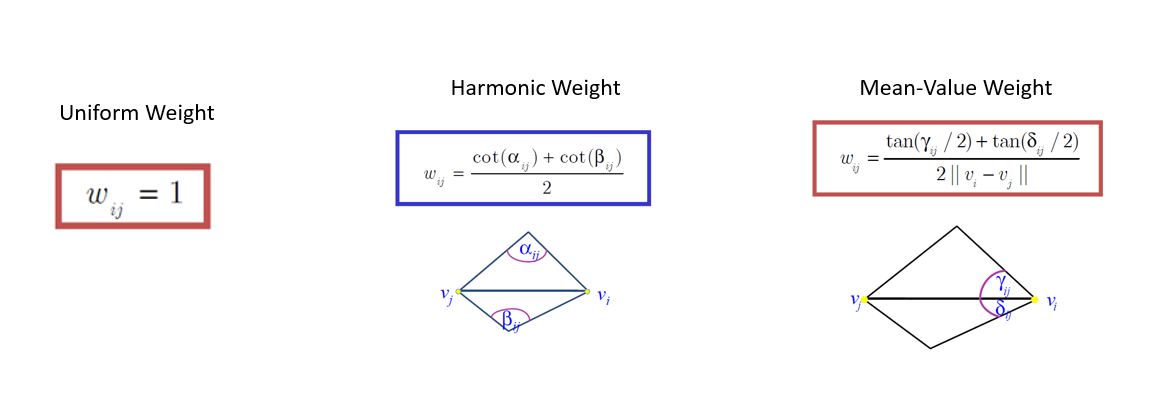
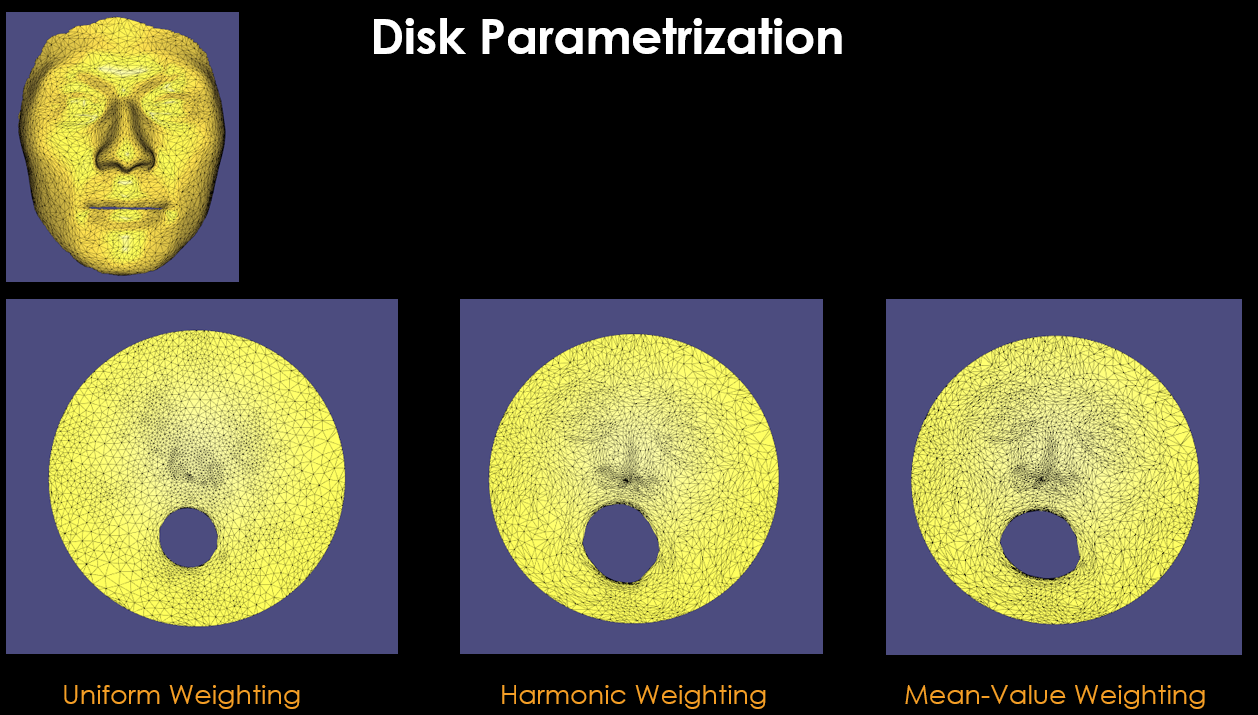
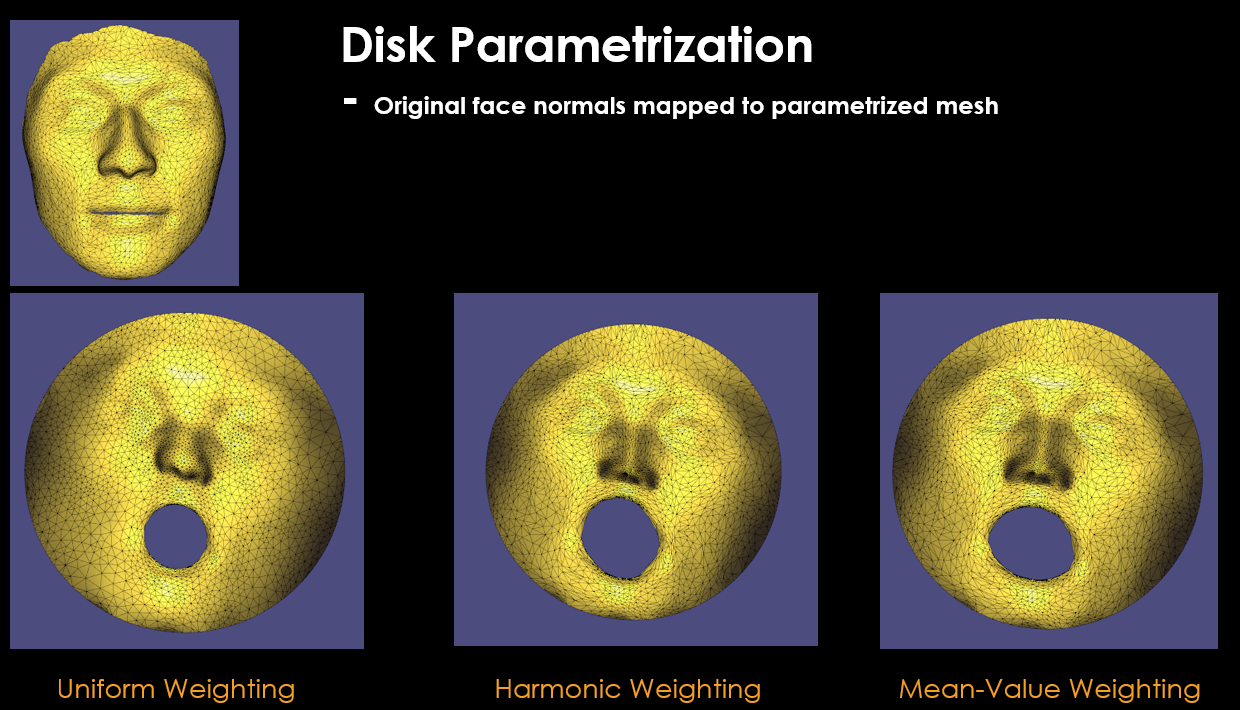
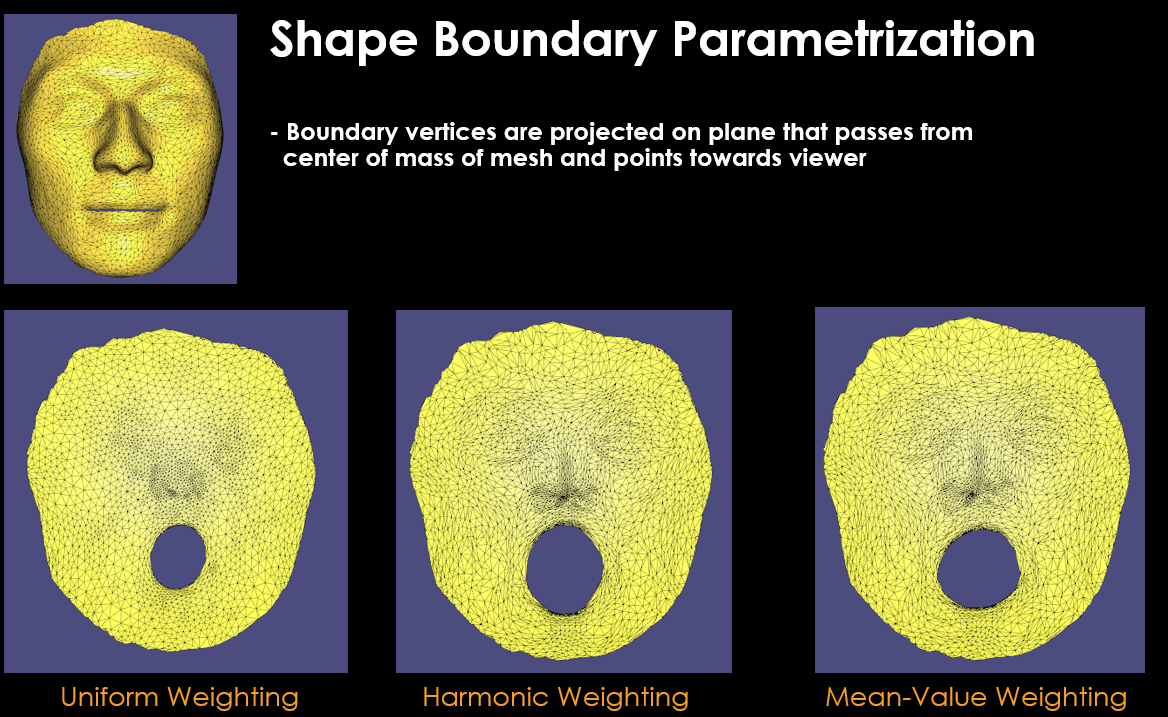
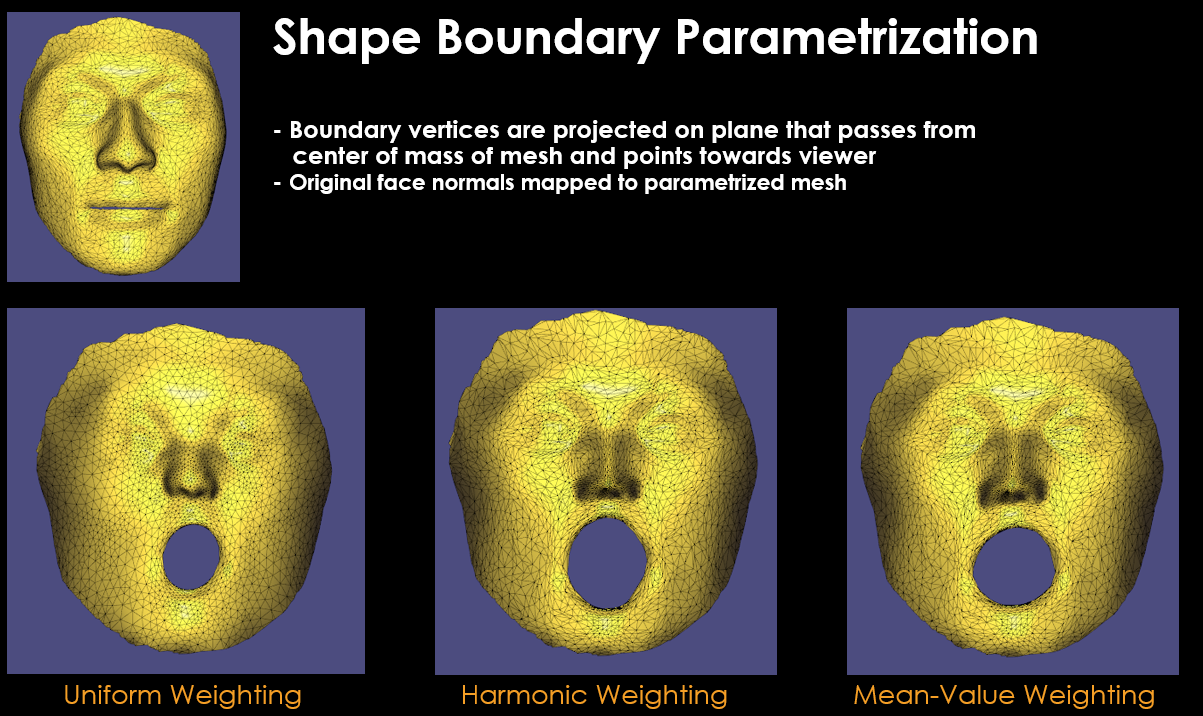
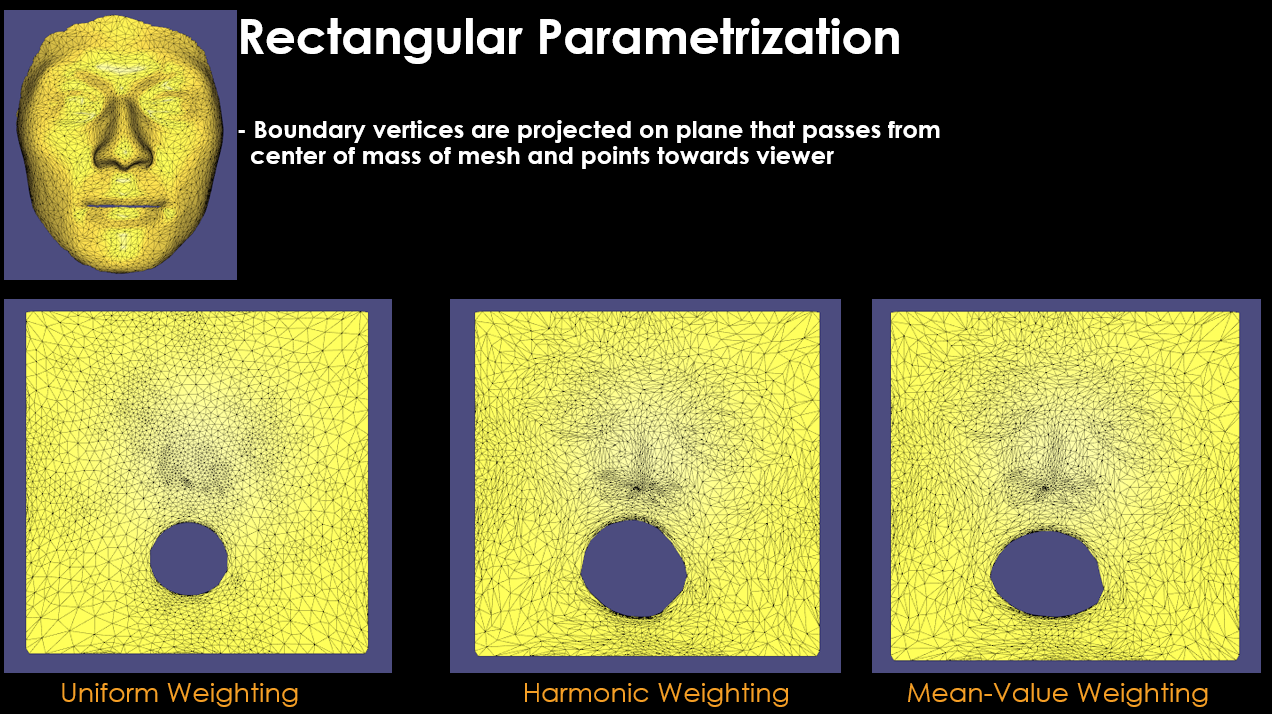
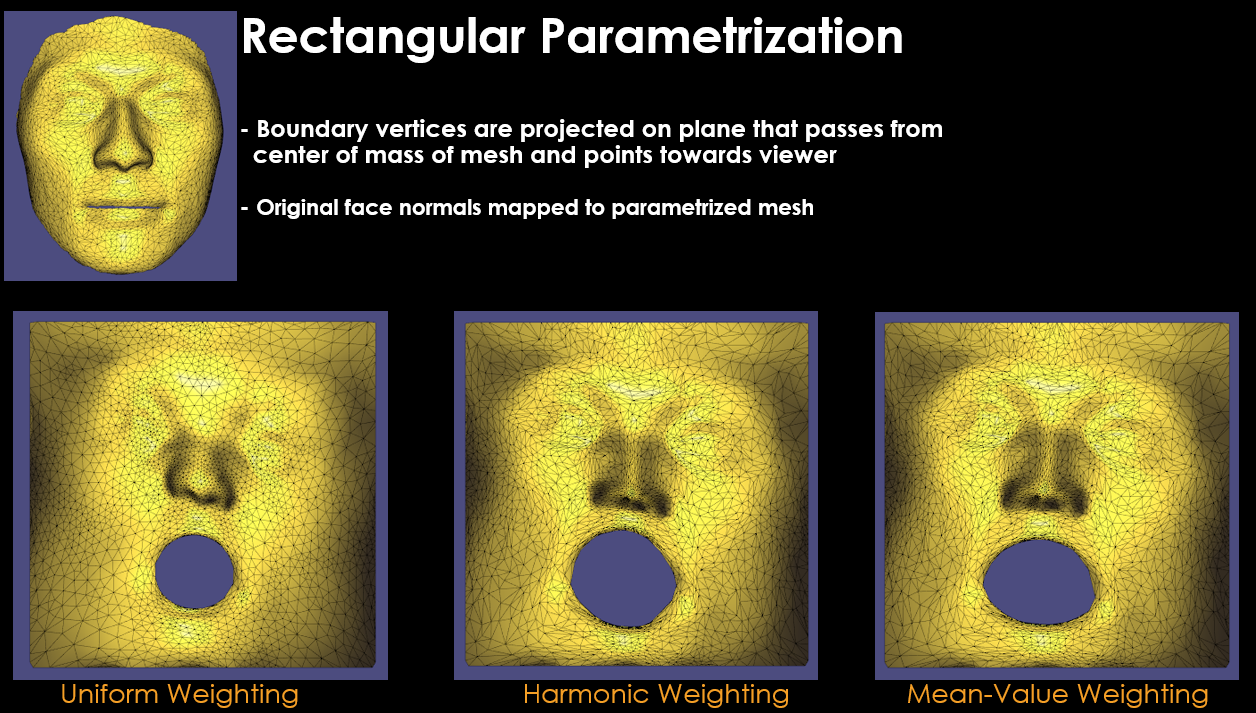
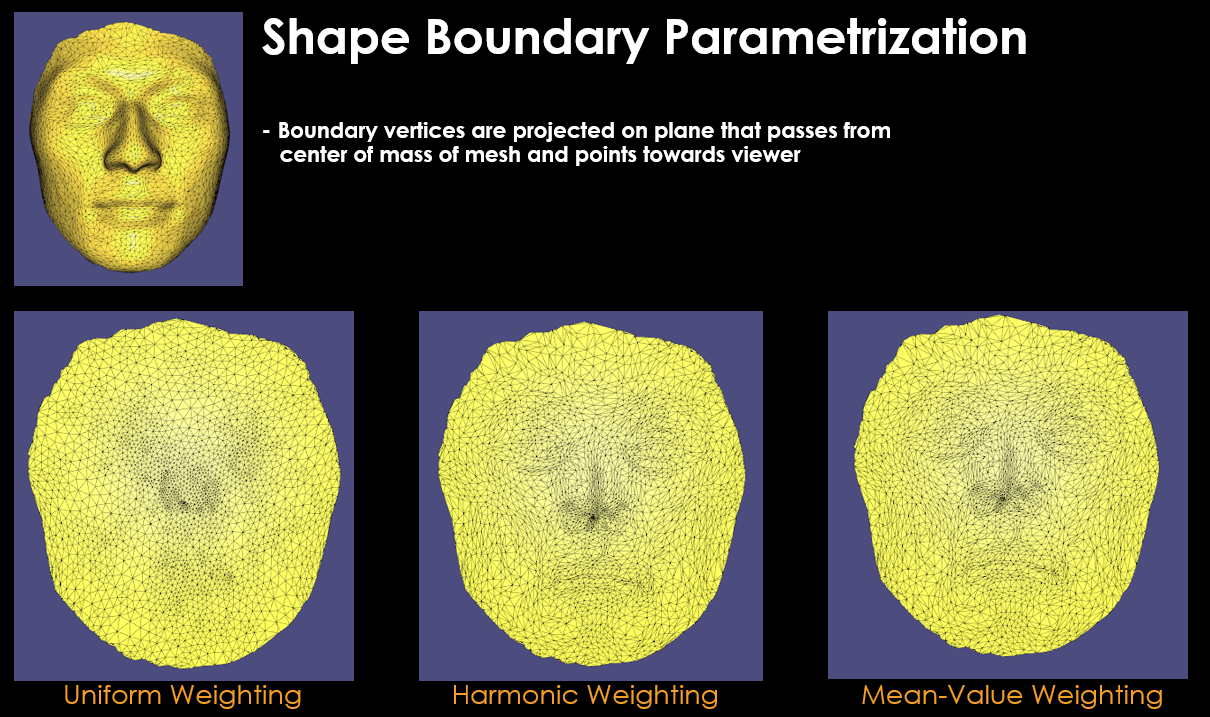
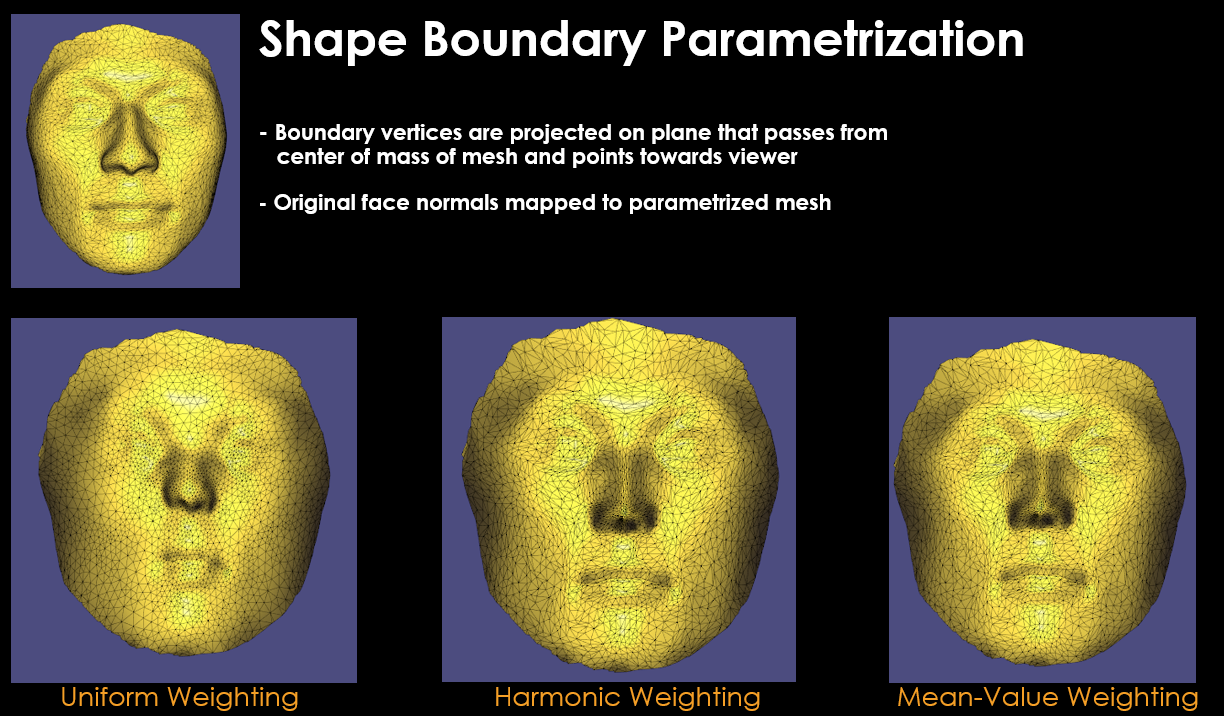
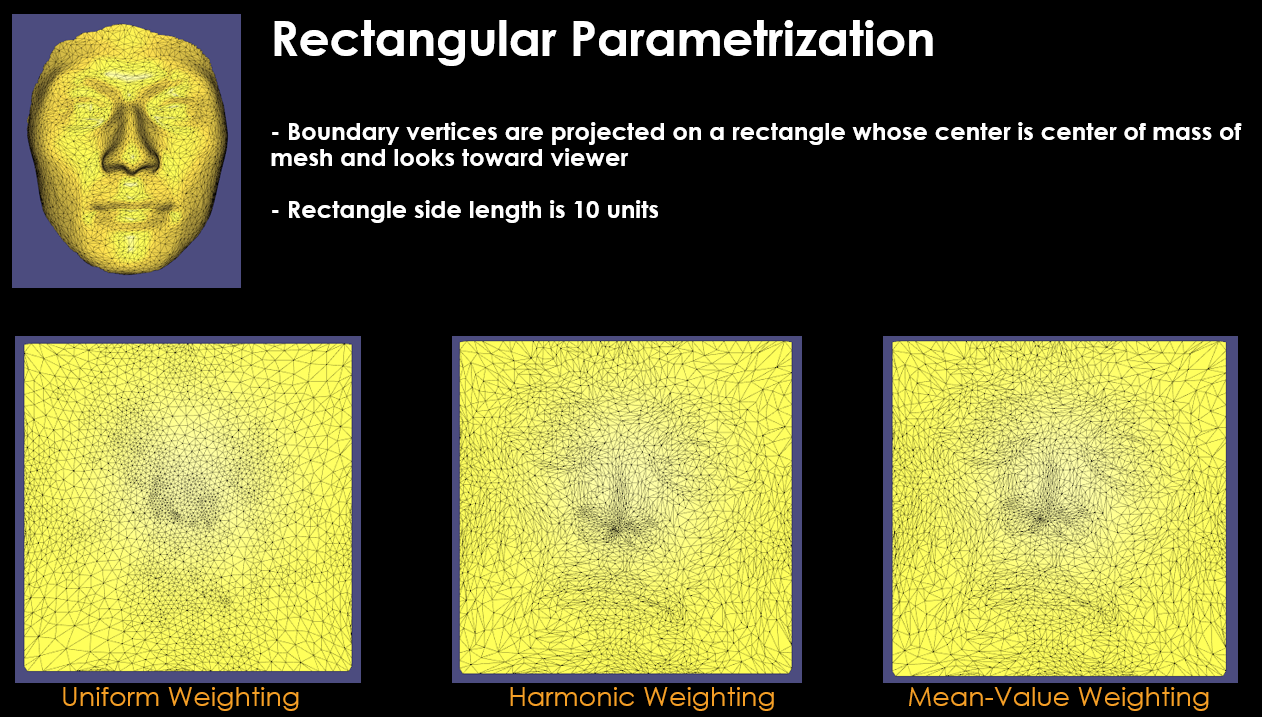
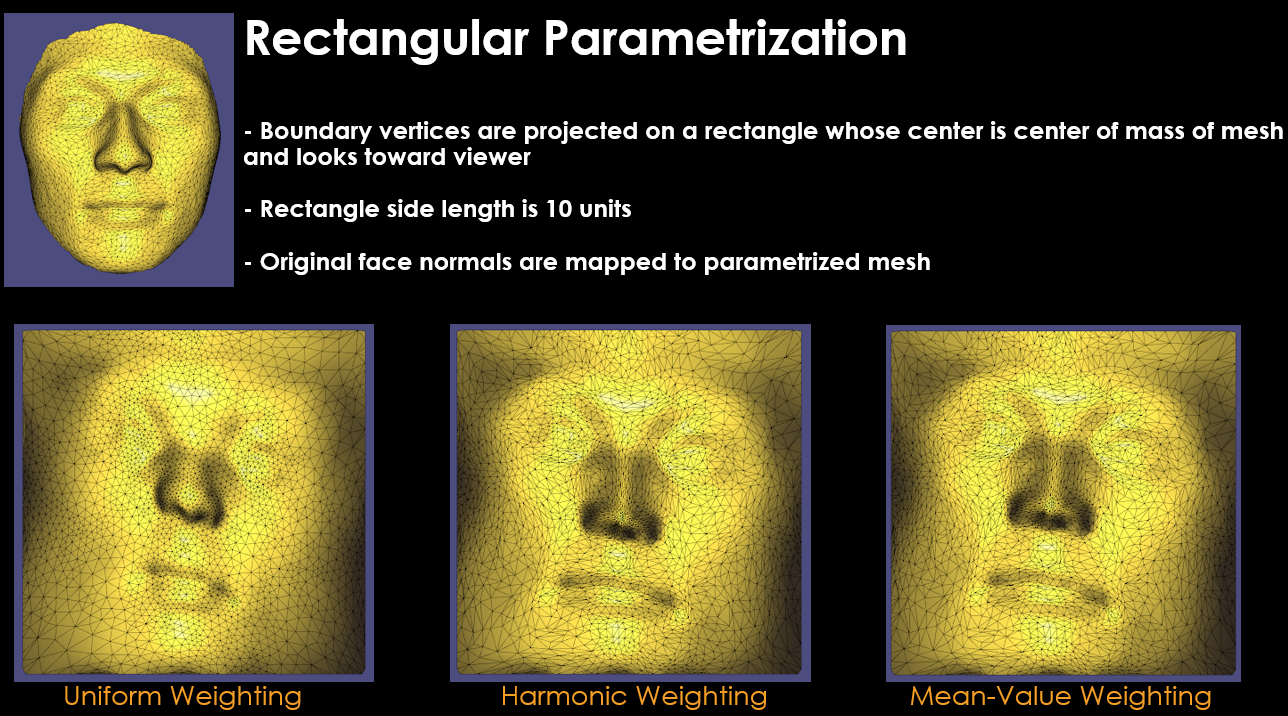
$W_{ij}$ weighting terms greatly affect the final parametrized mesh results. According to my research on literature [2], there exists different weighting functions used in mesh parametrization:
- Uniform weighting
- Harmonic weighting
- Mean-Value weighting
Each of these functions has its pros and cons that you can read if you wish in [2]. But mean-value weighting makes sure that final parametrized mesh is non-bijective ( means no vertex overlaps from original mesh in parametrized mesh ) which is a good metric for successful parametrization in my opinion.
In the remaining of this section I will share my implementation results for mesh parametrization:
In this post, I have made use of slides prepared by Assoc. Prof. Yusuf Sahillioğlu [3] for explaining linear system that solves mesh parametrization problem.
In this post, I have tried to share my journey in mesh parametrization, hope it was informative and you liked it $\triangle$
References:
1 - https://doc.cgal.org/latest/Surface_mesh_parameterization/index.html
3 - http://user.ceng.metu.edu.tr/~ys/ceng789-dgp/08-parameterization.ppt